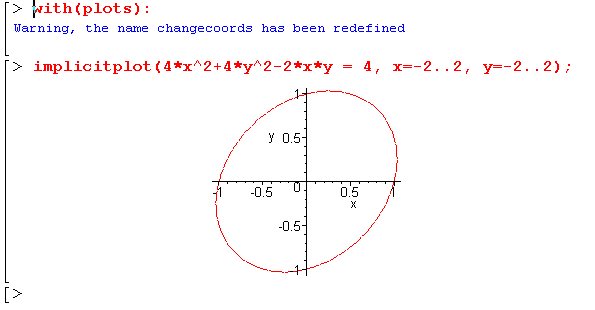Klausuren LA II

• Das Ergebnis der Endklausur.
• Die Aufgaben der Endklausur.
• Das Ergebnis der Nachklausur.
  Bemerkungen zur Klausur:

  (1) Hier eine Maple-Zeichnung der Ellipsen in Aufgabe 8 der Endklausur (die Ellipse der Aufgabe 8 der Nachklausur hat die gleichen Hauptachsen):
  

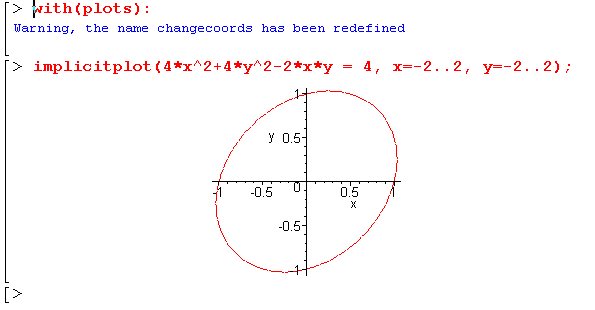
  (2) Nicht berücksichtigt wurde bei der Auswertung der Endklausur, dass die Antwort auf die Frage nach der Ordnung der Symmetriegruppe eines regelmäßen 7-Ecks durchgängig fehlerhaft war!
  Unter der Ordnung einer Gruppe G versteht man die Anzahl der Elemente von G, in diesem Fall ist die Ordnung von G also 14. Man darf dies nicht verwechseln mit der Ordnung von Elementen einer Gruppe. Die Ordnung eines Elements g einer Gruppe ist die Ordnung der von g erzeugten Untergruppe!

Bescheinigungen über die erfolgreiche Teilnahme

Hier eine genauere Liste der Kenntnisse, die erwartet wurden!

Die Probeklausur (über die ersten Teile der Vorlesung)

• Die Teile I, II, III der Vorlesung, also
  • Jordan'sche Normalform.
  • Faktorraum, Dualraum.
  • Euklid'sche Räume, unitäre Räume
    orthogonale und unitäre Endomrophsimen.
• Aufgaben im Stil der Übungsblätter 1-8 (aber einfacher).
• Routine-Rechnungen zu den Begriffen und Algorithmen.

Wie in der Vorlesung LA I kann man auf diese Weise Extrapunkte für die Endklausur sammeln, und zwar nach folgendem Schlüssel: Die Endklausur besteht aus zwei gleichgewichteten Teilen A und B, die Aufgaben von Teil A entsprechen denen der Probeklausur. Hat man x Punkte in der Probeklausur, und x' Punkte im Teil A der Endklausur, so wird als Gesamtergebnis für den Teil A die Formel max(x',x/4+x'/2) genommen.

Die Klausuren LA I

• Klausur: Samstag, 19.02.2005, 9:15, Audimax
  • Die Aufgaben
  • Die Ergebnisse
    Die korrigierten Klausur-Bearbeitungen können im Sekretariat (V5-210) gegen Unterschrift abgeholt werden.
• Wiederholungsklausur: Samstag, 19.03.2005, 9:15, Audimax.
  • Die Aufgaben
  • Die Ergebnisse
• Zweite Wiederholungsklausur: Samstag, 04.06.2005, 10:15, Audimax.
  • Die Aufgaben
  • Die Ergebnisse
• Bescheinigungen gibt es erst im April im Sekretariat.

Anforderungen

Teil I

• Die Aufgaben (leicht modifiziert)
• Die Ergebnisse

Verfahren

• Matrizen addieren, multiplizieren.
• Eine Matrix als Linearkombination der Basismatrizen E_ij schreiben.
• Eine Matrix in Zeilenstufenform bringen.
• Eine Matrix in Schubert-Normalform bringen.
• Eine invertierbare Matrix als Produkt von Elementarmatritzen und einer Diagonalmatrix schreiben
• Eine quadratische Matrix invertieren.
• Bestimmung, ob eine Permutation gerade oder ungerade ist (Berechnung der Anzahl der Fehlstellungen).
• Bestimmung des Produkts zweier Permutationen, des Inversen einer Permutation.
• Berechnung der Determinante einer quadratischen Matrix mit Koeffizienten in einem kommutative Ring.
• Berechnung der Spur einer quadratischen Matrix.
• Beweisen, dass ähnliche Matrizen A, B viele gleiche Eigenschaften haben.
  (Zum Beispiel: Ist A nilpotent, so auch B; ist A idempotent, so auch B; usw.).

• Nachweis, dass eine Untermenge einer Gruppe eine Untergruppe ist.
• Nachweis, dass eine Untermenge eines Rings ein Unterring ist.
• Nachweis, dass eine Abbildung f : G → H mit Gruppen G, H ein Gruppen-Homomorphismus ist.
• Nachweis, dass eine Abbildung f : R → S mit Ringen R, S ein Ring-Homomorphismus ist.

• Elementares Rechnen in Gruppen. (Zum Beispiel: Ist G eine Gruppe mit Einselement e und ist g ein Element in G, so folgt aus g⁵ = g³, dass gilt: g² = e. (Man multipliziert mit g^-3.))

Wissen

• Matrizen-Multiplikation ist nicht immer definiert.
• Matrizen-Multiplikation ist nicht kommutativ.
• Sind A, B n×n-Matrizen, so ist meist det(A+B) ≠ det A + det B.
• Wie ändert sich die Determinante einer Matrix, wenn man Zeilenoperationen durchführt?
• Definition der Ähnlichkeit von quadratischen Matrizen.
• Definition der komplementären Matrix zu einer quadratischen Matrix mit Koeffizienten in einem kommutativen Ring.

Teil II

• Die Aufgaben (leicht modifiziert)
• Die Ergebnisse

Verfahren

• Rechnen in Z/nZ: Addition, Multiplikation.
  Ist n Primzahl, so auch Division.
• Rechnen in C: Addition, Multiplikation, Division.
• Rechnen im Polynomring K[T], mit K Körper.
• In Z und in K[T]: Euklid'scher Algorithmus, Bestimmung des ggT,
  Bezout'sche Gleichung.

• Berechnung des charakteristischen Polynoms einer beliebigen quadratischen Matrix (mit Koeffizienten in einem kommutativen Ring)
• Bestimmung des Minimalpolynoms geeigneter Matrizen in M(n×n,K). (Dabei sei K ein Körper.)
  Insbesondere sollte Folgendes selbstverständlich sein: Gilt für eine Matrix A eine Bedingung wie etwa A⁵ = A², so ist A Nullstelle des Polynoms T⁵ - T²; das Minimalpolynom von A ist also ein Teiler von T⁵ - T².

  Sei K ein Körper.

• Überprüfen, ob eine Teilmenge von Kⁿ ein Unterraum ist.
• Gegeben sei eine Teilmenge S von Kⁿ. Bestimmung einer Basis von < S >.
• Sei S linear unabhängige Teilmenge eines Unterraums U von Kⁿ:
  • Ergänzung zu einer Basis von U.
  • Einen Vektor v in < S > als Linearkombintation der Vektoren in S schreiben.
  • Überprüfen, ob vorgegebene Vektoren linear abhängig oder linear unabhängig sind. (Um zu zeigen, dass eine Menge von Vektoren linear abhängig ist, gibt man, wenn möglich, eine nicht-triviale Linearkombination, die gleich Null ist, an.)
• Gegeben seien zwei Basen des Kⁿ. Berechnung der Basiswechselmatrix.

• Darstellung eines Unterraums von Kⁿ als Durchschnitt von Hyperflächen.
• Sei A eine (m×n)-Matrix mit Koeffizienten in K. Bestimmung einer Basis von Loes(A,0).
• Die Konstruktion von linear unabhängigen Vektoren mit Hilfe von Vandermonde-Matrizen.

• Bestimmung des Rangs einer Matrix.

Wissen

• Beispiele irreduzibler Polynome über Q, R, C, Z/2Z.

• Dass Vektorräume üblicherweise nicht nur eine Basis besitzen.
• Dass die mengentheoretische Vereinigung zweier Unterräume im allgemeinen kein Unterraum ist! (mit Beweis!)
• Die Dimensionsformel für Paare von Unterräumen eines Vektorraums
• Die Modularitätsformel (für Tripel U₁, U₂, U₃ von Unterräumen eines Vektorraums, falls U₁ in U₃ enthalten ist)
  (mit Beweis!, und man sollte auch entsprechende Beweise für andere Inklusionsbeziehungen von Unterräumen führen könenn).

Teil III: Lineare Abbildungen

Verfahren

• Die Zuordnung einer Matrix zu einer linearen Abbildung f : V → W (dabei sind V, W endlich-dimensionale Vektorräume), falls in V und in W jeweils eine Basis gegeben ist.
• Bestimmung von Kern (und Bild) einer linearen Abbildung.
• Bestimmung des Rangs einer linearen Abbildung.
  Wie verhält sich der Rang der Hintereinanderschaltung zweier linearen Abbildungen zum Rang der beiden Abbildungen?

• Die Zuordnung einer Matrix zu einem Endomorphismus f : V → V (dabei sei V endlich-dimensionaler Vektorraum), falls in V eine Basis gegeben ist.
• Die Berechnung von Eigenwerten und zugehörigen Eigenvektoren eines Endomorphismus.
• Die Bestimmung von f-invarianten Unterräumen eines Endomorphismus f.

Wissen

• Ganz allgemein sollte man den Zusammenhang zwischen linearen Abbildungen und Matrizen kennen.
• Die Dimensionsformel für Kern und Bild einer linearen Abbildung.
• Eine lineare Abbildung ist genau dann injektiv, wenn ihr Kern gleich 0 ist.

• Ein Endomorphismus eines endlich-dimensionalen Vektorraums ist genau dann injektiv, wenn er surjektiv ist.
• Die Frage, ob ein Endomorphismus Eigenwerte (und demnach Eigenvektoren) hat, hängt ganz entscheidend vom Grundkörper ab!
  Betrachtet man zum Beispiel eine 2×2-Drehmatrix A als Matrix in M(2×2,R), so hat sie im allgemeinen keinen Eigenwert (außer ....), dagegen hat die gleiche Matrix A als Element von M(2×2,C) immer Eigenwerte!
• Ist f ein Endomorphismus eines n-dimensionalen Vektorraums, so impliziert die Existenz von n paarweise verschiedenen Eigenwerten, dass f diagonalisierbar ist.

• Die Matrix-Darstellung einer Drehung der reellen Ebene um den Ursprung.
• Die Matrix-Darstellung einer Spiegelung der reellen Ebene an einer Geraden durch den Ursprung.

Last modified: Sun Jul 3 09:12:09 CEST 2005