Jede Woche (meist zum Wochenende hin) sollen an dieser Stelle einige Highlights
des kommenden Bundeskongresses und Informationen über Bielefeld und
Umgebung vorgestellt werden -
soweit möglich thematisch gebündelt.
|
|
| Mathematik zum Anfassen
|
|
Im Rahmen des Bundeskongresses werden in einer
Ausstellung
einige Exponate der Wanderausstellung Mathematik zum Anfassen des
Mathematikums in Gießen
gezeigt. Mathematik zum Anfassen stellt
den Besuchern interaktive Exponate zur Verfügung:
Besucher jeden Alters und jeder Vorbildung experimentieren -
sie legen Puzzles,
bauen Brücken, zerbrechen sich den Kopf bei Knobelspielen,
schauen einem Kugelwettrennen zu und vieles mehr. Das heißt:
Die Besucher führen alleine oder in Gruppen selbständig Experimente
durch und erleben so ganz direkt und unmittelbar mathematische Phänomene.
|


|
Die Experimente
- Leonardo-Brücke
- Penrose-Puzzle
- Pythagoras zum Wiegen
- Seifenhaut-Tisch
- Spiegelbuch
- Wo geht's am schnellsten runter?
- Würfelschlange
- Der Zweite ist immer der Erste
|
- Alle Dreiecke sind gleich
- Ich bin eine Funktion
|
|
|
- 2er-Pyramide
- Kugelpyramide
- 4er-Pyramide
- Das T
- Waben
- Zwerge
|
|
| Das teutolab Mathematik
|
Hier soll auch kurz über das
teutolab Mathematik berichtet werden, das entsprechende
Experimente für Schülerinnen und Schüler zur Verfügung
stellt:
- Spiegelungen
- Geheimschriften
- Bauwas
- Das Galtonbrett
- Platonische Körper
- Die Murmelbahn
- Rechentricks
- Die Ellipse
|
|


|
zusätzlich zum eigenständigen Experimentieren der Kinder werden
hier anschließend die Entdeckungen der Kinder mit ihnen diskutiert und
eingeordnet. Im Vortrag TM 30.01 von Lena Fischer und im Workshop TM 30.02
unter der Leitung von Peter Rasfeld werden Konzeption und Erfahrungen dieses
Schülerlabors beschrieben; alle teutolabs können am Dienstag
nachmittag besichtigt und die Materialien erprobt werden.
|
| Puzzles und Mathematik
|
|
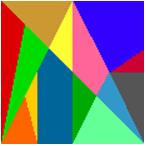
In den Workshops Puzzles und Mathematik (WM 29.02 und WM 31.03,
unter Leitung von Bernhard Schweitzer) werden einige Knobel-Denkspiele vorgestellt
und die dazugehörige Mathematik analysiert. Zum Beispiel das Stomachion
des Archimedes, das als das älteste Puzzle der Welt gilt: 11 Dreiecke,
zwei Vierecke und ein Fünfeck sind zu einem Quadrat zusammenzufügen.
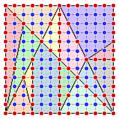
Neuere Forschungen zeigen, dass sich schon Archimedes dafür interessierte,
wie viele wesentlich verschiedene Lösungen es gibt. Die Antwort ist
536. Und man kann zeigen, dass bei allen Lösungen die Eckpunkte der
Einzelteile auf einem 12×12-Gitter liegen.
|
|
Mehr über das Stomachion.
|
|
Zaubern
|
|
Die von Wolfgang Hund geleiteten Workshops WM 29.03 und WM 31.02
tragen den Titel Zauberhafte Mathematik: Zauberhaftes Lernen im Mathematikunterricht.
In diesen Veranstaltungen soll anhand
von Beispielen aufgezeigt (und mit den Teilnehmern durchgeführt) werden,
wie die Motivationskraft von Zauberkunststücken
im Mathematik-Unterricht nutzbar gemacht werden kann.
|
|
Neulich war ich mit 20 Schülern in einem Raum, in dem sich nur 19 Stühle befanden.
Alle Schüler sollten natürlich sitzen. Was tat ich?
Ich stellte die Stühle in einer Reihe auf und setzte den ersten Schüler
auf den ersten Stuhl.
Dann fragte ich ihn, ob sich ein paar Minuten lang noch jemand neben ihn
(also auf seinen Stuhl) setzen dürfte.
Ich nahm einen anderen Schüler und beide teilten sich die Sitzfläche.
Den dritten Schüler setzte ich auf den zweiten Stuhl,
den vierten Schüler auf den dritten Stuhl,
den fünften Schüler auf den vierten Stuhl.
Usw, usw.
Den achtzehnten Schüler setzte ich auf den siebzehnten Stuhl,
den neunzehnten Schüler auf den achtzehnten Stuhl.
Dann holte ich noch den zwanzigsten Schüler,
der zusammen mit dem ersten auf dem ersten Stuhl ausharrte und setzte ihn auf den
neunzehnten Stuhl.
Damit waren alle 20 Schüler untergebracht!
|
|
|
| Die Modellsammlung der Fakultät für Mathematik
|






|
|
Welche Modelle kann man in der Bielefelder Modellsammlung (in Vitrinen in V3)
besichtigen? Es gibt eine
vielfältige Polyeder-Sammlung: neben den regulären
dreidimensionalen Polyedern (also den platonischen Körpern,
wie den fünf nicht-konvexen Körpern,
den Kepler-Poinsot-Körpern) findet man alle archimedischen Körper
und die dazu dualen Körper, aber auch dreidimensionale Projektionen
vierdimensionaler regulärer Polyeder (etwa das 120-Zell: man sieht seinen
dreidimensionalen Rand, nämlich 120 Dodekaeder,
deren Seitenflächen jeweils paarweise identifiziert sind).
Dann gibt es verschiedenartige Modelle der reellen Quadriken: Ellipsoide,
einschalige und zweischalige Hyperboloide (das einschalige
kennt man als Grundform eines Kühlturms),
parabolische und hyperbolische Paraboloide (Parabolspiegel, Dachkonstruktion);
gezeigt wird dabei, inwieweit auf diesen Flächen Geradenscharen
oder Kreisscharen liegen. Entsprechend sieht man,
wie man einen Torus (Rettungsring) durch Kreise erzeugen kann:
neben den zwei offensichtlichen Möglichkeiten gibt es eine dritte,
die in der theoretischen Mathematik als Hopf-Faserung
eine besondere Rolle spielt. Und auch Fadenmodelle von
Kurven im dreidimensionalen Raum, aber auch
die mögliche Färbungen von Triangulierungen einer Brezelfläche.
|
| Die 27 Geraden
|

Bielefelder Modell
der Clebschen Fläche
|
Besonders stolz ist Bielefeld aber auf zwei Modelle,
die einem Thema gewidmet sind, das schon im 19.Jahrhundert viel
diskutiert wurde und jetzt in ziemlich allen Lehrbüchern zur
algebraischen Geometrie einen besonderen Rang einnimmt:
den 27 Geraden auf einer kubischen Fläche im Raum.
Cayley und Salmon haben 1849 bewiesen, dass es auf einer glatten Fläche,
die durch ein Polynom 3.Grads definiert ist, immer genau 27 Geraden gibt
(ein völlig überraschendes Ergebnis), und dass jede
dieser Geraden genau 10 der übrigen schneidet.
Clebsch (und Klein) konstruierten dann 1872 ein Modell,
das weltberühmt wurde: es wurde 1894 als deutscher
Beitrag auf der Weltausstellung in Chicago gezeigt.
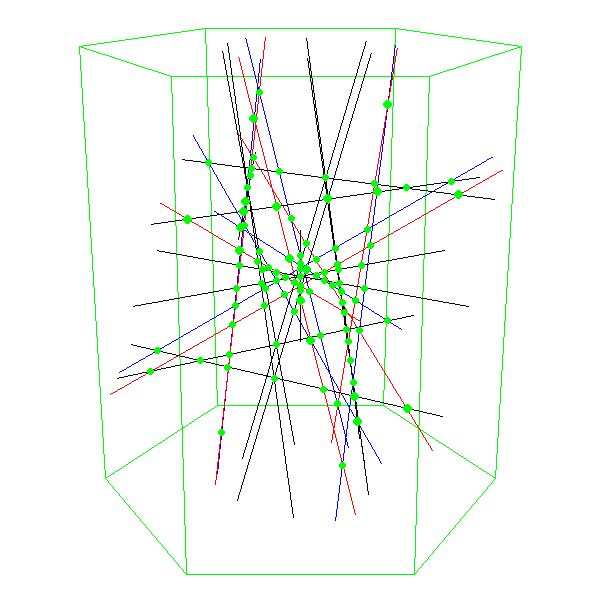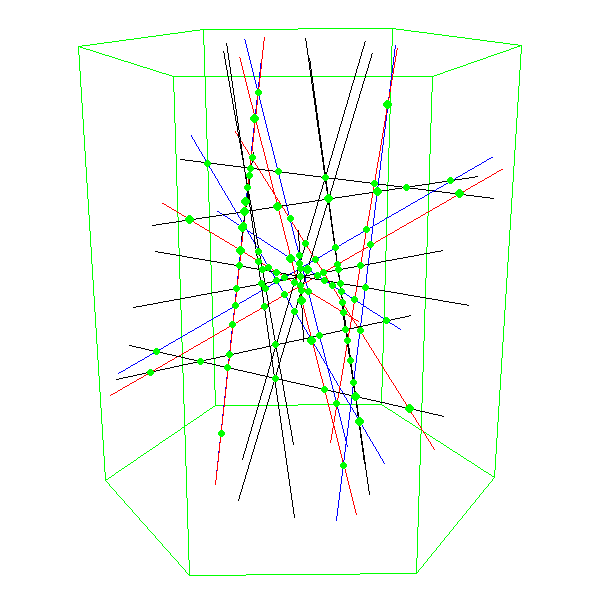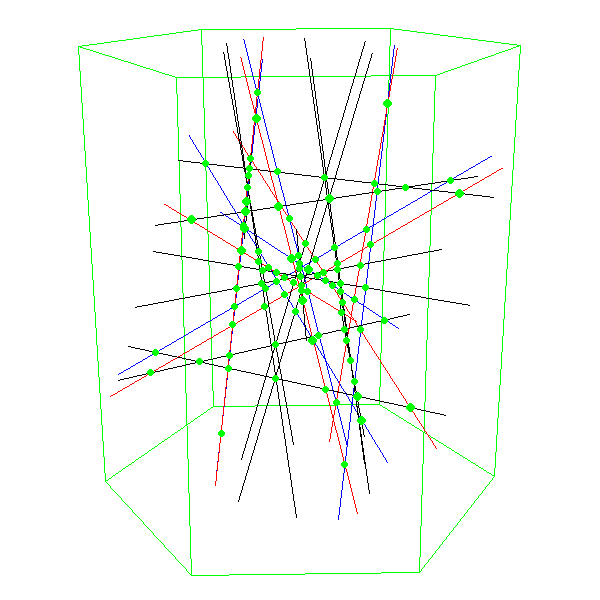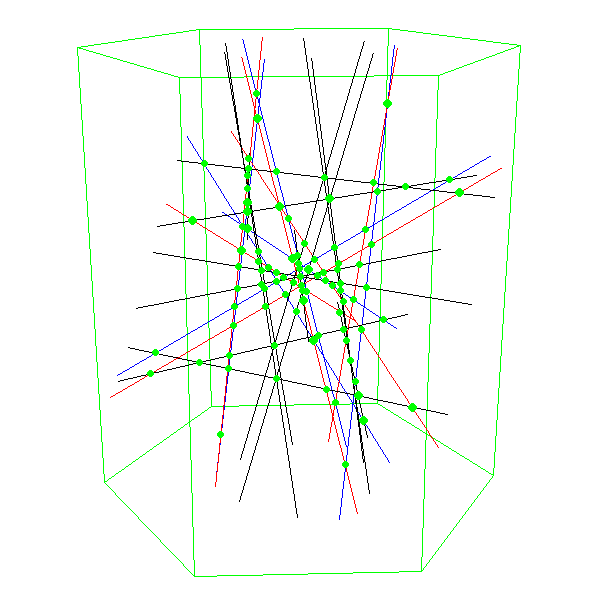
Seit 2009 gibt es in der Bielefelder Modellsammlung nun auch ein Modell
der Konfiguration der 27 Geraden, das eindringlich
das Schnittverhalten der Geraden zeigt, ohne dass man von der
ja ansonsten durchaus beeindruckenden Fläche abgelenkt wird.
|
|
|
|
Die virtuelle Vorlage für das Modell der 27 Geraden (Beineke, Kürpig, Ringel)
|
|
|













