Prof. Dr. William (=Bill) Crawley-Boevey
Alexander von Humboldt Professor
Research group: BIREP
E-Mail: wcrawley
Telephone: +49 (0)521 106 5033
Office: V5-221
Teaching
CRC
I am a participant in
Collaborative Research Centre 358
on "Integral Structures in Geometry and Representation Theory".
I am a principal investigator on projects
A6,
C2,
C3.
Miscellaneous
Distinctions
Editorial Work
Research Students
- Roberto Vila Freyer completed an Oxford D. Phil. on the topic 'Biserial algebras' in 1994.
- Nicola Richmond completed a Leeds Ph. D. on the topic 'The geometry of modules over finite dimensional algebras' in 1999.
- Andrew Hubery completed a Leeds Ph. D. on the topic 'Representations of quivers respecting a quiver automorphism and a theorem of Kac' in 2002.
- Peter Shaw
completed a Leeds Ph. D. on the topic 'Generalisations of Preprojective algebras' in 2005. pdf.
- Marcel Wiedemann completed a Leeds Ph. D. on the topic 'On real root representations of quivers' in 2008. pdf.
- Daniel Kirk completed a Leeds Ph. D. on the topic 'Representations of Quivers with Applications to Collections of Matrices with Fixed Similarity Types and Sum Zero' in 2013. pdf.
- Raphael Bennett-Tennenhaus completed a Leeds Ph. D. on the topic 'Functorial Filtrations for Semiperfect generalisations of Gentle Algebras' in 2017. pdf.
- Ulrike Hansper completed a Bielefeld Ph. D. on the topic 'Classification of the indecomposable finite dimensional modules of clannish algebras' in 2021/22. pdf.
- Sebastian Eckert completed a Bielefeld Ph. D. on the topic 'Hyperfinite families, amenable representation type and non-amenability of controlled wild algebras' in 2022. pdf.
- Vincent Klinksiek started a Bielefeld Ph. D. in November 2019.
Humboldt Award
The research group was supported by the Alexander von Humboldt Stiftung/Foundation in the framework of the Alexander von Humboldt Professorship endowed by the Federal Ministry of Education and Research.
The grant ran from October 2016 until 2021.
Research Interests
My research has mainly been on the representation theory of finite-dimensional associative algebras
(see fdlist),
and related questions in linear algebra, ring and module theory, and algebraic geometry.
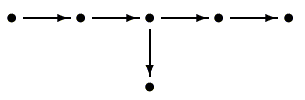 In recent years I have concentrated on representations of quivers and
preprojective algebras. A quiver is essentially the same
thing as a directed graph,
and a representation associates a vector space to each vertex
and a linear map to each arrow. The subject was started by P. Gabriel
in 1972, when he discovered that the
quivers with only finitely many indecomposable representations are exactly
the ADE Dynkin diagrams which occur in Lie theory (for example a quiver of
type
E6 is illustrated on the left).
Quivers and their representations now appear in all sorts of
areas of mathematics and physics,
including representation theory, cluster algebras, geometry (algebraic,
differential, symplectic), noncommutative geometry,
quantum groups, string theory, and more.
In recent years I have concentrated on representations of quivers and
preprojective algebras. A quiver is essentially the same
thing as a directed graph,
and a representation associates a vector space to each vertex
and a linear map to each arrow. The subject was started by P. Gabriel
in 1972, when he discovered that the
quivers with only finitely many indecomposable representations are exactly
the ADE Dynkin diagrams which occur in Lie theory (for example a quiver of
type
E6 is illustrated on the left).
Quivers and their representations now appear in all sorts of
areas of mathematics and physics,
including representation theory, cluster algebras, geometry (algebraic,
differential, symplectic), noncommutative geometry,
quantum groups, string theory, and more.
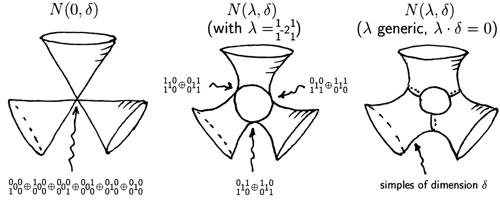 The preprojective algebra associated to
a quiver was invented by I. M. Gelfand and V. A. Ponomarev.
Its modules are intimately related to representations of the quiver, but it is
often the modules for the preprojective algebra which are of relevance in other
parts of mathematics. There is beautiful geometry linked to the preprojective algebra,
including Kleinian singularities and H. Nakajima's quiver varieties. (The
illustration on the right shows the real-valued points of
varieties associated to a quiver of extended Dynkin, that is,
affine, type D4.)
The preprojective algebra associated to
a quiver was invented by I. M. Gelfand and V. A. Ponomarev.
Its modules are intimately related to representations of the quiver, but it is
often the modules for the preprojective algebra which are of relevance in other
parts of mathematics. There is beautiful geometry linked to the preprojective algebra,
including Kleinian singularities and H. Nakajima's quiver varieties. (The
illustration on the right shows the real-valued points of
varieties associated to a quiver of extended Dynkin, that is,
affine, type D4.)
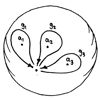 There are also links between the preprojective algebra and
the classification of differential equations on the Riemann
sphere. They are used in work on the Deligne-Simpson problem,
which concerns the existence of matrices
in prescribed conjugacy classes whose product is
the identity matrix, or whose sum is the zero matrix.
(The picture on the left shows loops on the punctured Riemann sphere which
generate its fundamental group. Consideration of the monodromy around
such loops links
the classification of differential equations on the Riemann sphere
to the Deligne-Simpson problem.)
There are also links between the preprojective algebra and
the classification of differential equations on the Riemann
sphere. They are used in work on the Deligne-Simpson problem,
which concerns the existence of matrices
in prescribed conjugacy classes whose product is
the identity matrix, or whose sum is the zero matrix.
(The picture on the left shows loops on the punctured Riemann sphere which
generate its fundamental group. Consideration of the monodromy around
such loops links
the classification of differential equations on the Riemann sphere
to the Deligne-Simpson problem.)
In earlier times I was interested in tame algebras, matrix problems, and
infinite-dimensional modules. Finite dimensional associative algebras naturally
divide into three classes: algebras finite representation
type with only finitely many indecomposable modules,
wild algebras for which the indecomposable modules are unclassifiable
(in a suitable sense), and those on the boundary between these classes, the
tame algebras. There are many interesting classes of tame algebras,
and it is often a major problem to actually give the classification of the
indecomposable modules.
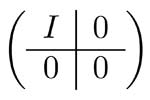 One way to study tame algebras is to convert the problem of classifying their
modules into a matrix problem: putting a partitioned matrix into
canonical form using not all elementary operations, but a subset defined
by the partition.
(The illustration on the right shows what an arbitrary matrix can be
reduced to if you allow all row and column operations; it also shows an
example of a partition of a matrix.)
Using advanced methods based on this idea, Yu. A. Drozd
proved
his wonderful Tame and Wild Theorem showing that there is a wide gulf between
the behaviour of tame and wild algebras.
The same methods can be used to show that tame algebras are characterized by
the behaviour of their infinite-dimensional modules. In fact, the behaviour of
infinite-dimensional modules for tame algebras is extremely interesting, and
not at all understood.
One way to study tame algebras is to convert the problem of classifying their
modules into a matrix problem: putting a partitioned matrix into
canonical form using not all elementary operations, but a subset defined
by the partition.
(The illustration on the right shows what an arbitrary matrix can be
reduced to if you allow all row and column operations; it also shows an
example of a partition of a matrix.)
Using advanced methods based on this idea, Yu. A. Drozd
proved
his wonderful Tame and Wild Theorem showing that there is a wide gulf between
the behaviour of tame and wild algebras.
The same methods can be used to show that tame algebras are characterized by
the behaviour of their infinite-dimensional modules. In fact, the behaviour of
infinite-dimensional modules for tame algebras is extremely interesting, and
not at all understood.
Publications
Google
Scholar page
-
Polycyclic-by-finite affine group schemes,
Proc. London Math. Soc., 52 (1986), 495-516.
(doi).
-
Locally finite representations of groups of finite p-rank,
J. London Math. Soc., 34 (1986), 17-25.
(doi).
-
(With P. H. Kropholler and P. A. Linnell) Torsion-free soluble groups and the zero-divisor conjecture,
J. Pure and Appl. Algebra, 54 (1988), 181-196.
(doi).
-
On tame algebras and bocses,
Proc. London Math. Soc., 56 (1988), 451-483.
(doi).
-
Functorial filtrations and the problem of an idempotent and a square zero matrix,
J. London Math. Soc., 38 (1988), 385-402.
(journal).
-
Functorial filtrations II: clans and the Gelfand problem,
J. London Math. Soc., 40 (1989), 9-30.
(doi).
-
Functorial filtrations III: semidihedral algebras,
J. London Math. Soc., 40 (1989), 31-39.
(doi).
-
Maps between representations of zero-relation algebras,
J. Algebra, 126 (1989), 259-263.
(doi).
-
(With L. Unger) Dimensions of Auslander-Reiten translates for representation-finite algebras,
Comm. Algebra, 17 (1989), 837-842.
(doi).
-
Matrix problems and Drozd's theorem, in 'Topics in Algebra',
eds S. Balcerzyk et al., Banach Center publications, vol. 26 part 1 (PWN-Polish Scientific Publishers, Warsaw, 1990), 199-222.
(pdf).
-
Regular modules for tame hereditary algebras,
Proc. London Math. Soc., 62 (1991), 490-508.
(doi).
-
Tame algebras and generic modules,
Proc. London Math. Soc., 63 (1991), 241-265.
(doi).
-
Lectures on representation theory and invariant theory,
Ergänzungsreihe Sonderforschungsbereich 343 'Diskrete Strukturen in der Mathematik', 90-004, Bielefeld University, 1990, 74pp.
(pdf).
-
Matrix reductions for artinian rings, and an application to rings of finite representation type,
J. Algebra, 157 (1993), 1-25.
(doi).
-
(With C. M. Ringel) Algebras whose Auslander-Reiten quiver has a large regular component,
J. Algebra, 153 (1992), 494-516.
(doi).
-
(With D. Happel and C. M. Ringel) A bypass of an arrow is sectional,
Arch. Math. (Basel), 58 (1992), 525-528.
(doi).
-
Modules of finite length over their endomorphism rings, in 'Representations of algebras and related topics',
eds H. Tachikawa and S. Brenner, London Math. Soc. Lec. Note Series 168, (Cambridge University Press, 1992), 127-184.
(pdf).
-
Additive functions on locally finitely presented Grothendieck categories,
Comm. Algebra, 22 (1994), 1629-1639
(doi).
-
Locally finitely presented additive categories,
Comm. Algebra, 22 (1994), 1641-1674.
(doi).
-
Exceptional sequences of representations of quivers, in 'Representations of algebras',
Proc. Ottawa 1992, eds V. Dlab and H. Lenzing, Canadian Math. Soc. Conf. Proc. 14 (Amer. Math. Soc., 1993), 117-124.
(pdf).
-
(With O. Kerner) A functor between categories of regular modules for wild hereditary algebras,
Math. Ann., 298 (1994), 481-487.
(doi,
GDZ).
-
(With D. J. Benson) A ramification formula for Poincaré series, and a hyperplane formula for modular invariants,
Bull. London Math. Soc., 27 (1995), 435-440.
(doi).
-
Subrepresentations of general representations of quivers,
Bull. London Math. Soc., 28 (1996), 363-366.
(doi).
-
(With R. Vila-Freyer) The structure of biserial algebras,
J. London Math. Soc., 57 (1998), 41-54.
(doi).
-
Rigid integral representations of quivers, in 'Representations of algebras',
Proc. Cocoyoc 1994, eds R. Bautista et al., Canad. Math. Soc. Conf. Proc., 18 (Amer. Math. Soc., 1996), 155-163.
(pdf).
-
Tameness of biserial algebras,
Arch. Math. (Basel), 65 (1995), 399-407.
(doi).
-
On homomorphisms from a fixed representation to a general representation of a quiver,
Trans. Amer. Math. Soc., 348 (1996), 1909-1919.
(doi).
-
(With M. P. Holland)
Noncommutative deformations of Kleinian singularities,
Duke Math. J., 92 (1998), 605-635.
(doi).
-
Infinite-dimensional modules in the representation theory of
finite-dimensional algebras,
Canadian Math. Soc. Conf. Proc., 23 (1998), 29-54.
(pdf).
-
Preprojective algebras, differential operators
and a Conze embedding for deformations of
Kleinian singularities,
Comment. Math. Helv., 74 (1999), 548-574.
(doi,
pdf).
-
(With R. Bautista, T. Lei and Y. Zhang)
On Homogeneous Exact Categories,
J. Algebra, 230 (2000), 665-675.
(doi).
-
On the exceptional fibres of Kleinian singularities,
Amer. J. Math., 122 (2000), 1027-1037.
(doi,
pdf).
-
Geometry of the moment map for representations of quivers,
Compositio Math., 126 (2001), 257-293.
(doi,
pdf).
-
Decomposition of Marsden-Weinstein reductions for representations of
quivers,
Compositio Math., 130 (2002), 225-239.
(doi,
math.AG/0007191).
-
(with Christof Geiß) Horn's problem and semi-stability for
quiver representations, in 'Representations of Algebras, Vol 1',
Proceedings of the Ninth International Conference, Beijing,
August 21-September 1, 2000, eds. D. Happel and Y. B. Zhang
(Beijing Normal University Press, 2002), 40-48.
(pdf).
-
(with Jan Schröer)
Irreducible components of varieties of modules,
J. Reine Angew. Math. 553 (2002), 201-220.
(doi,
math.AG/0103100).
-
Normality of Marsden-Weinstein reductions for representations
of quivers,
Math. Ann. 325 (2003), 55-79.
(doi,
math.AG/0105247).
-
On matrices in prescribed conjugacy classes with no common invariant
subspace and sum zero,
Duke Math. J. 118 (2003), 339-352.
(doi,
math.RA/0103101).
-
(with Michel Van den Bergh) Absolutely indecomposable representations and
Kac-Moody Lie algebras (with an appendix by Hiraku Nakajima),
Invent. Math. 155 (2004), 537-559.
(doi,
pdf).
-
Indecomposable parabolic bundles and the existence of matrices in
prescribed conjugacy class closures with product equal
to the identity, Publ. Math. Inst. Hautes Etudes Sci. 100 (2004), 171-207.
(doi,
NUMDAM).
-
(with Peter Shaw)
Multiplicative preprojective algebras, middle convolution
and the Deligne-Simpson problem, Adv. Math. 201 (2006), 180-208.
(doi).
-
(With Bernt Tore Jensen)
A note on sub-bundles of vector bundles, Glasgow Math. J. 48 (2006), 459-462.
(doi,
pdf).
-
Quiver algebras, weighted projective lines, and the Deligne-Simpson
problem, in: 'Proceedings of the International Congress of Mathematicians', vol. 2,
Madrid 2006, eds M. Sanz-Solé et al.
(European Mathematical Society, January 2007), 117-129.
(pdf).
-
(With Pavel Etingof and Victor Ginzburg)
Noncommutative Geometry and Quiver algebras, Adv. Math. 209 (2007), 274-336.
(doi).
-
General sheaves over weighted projective lines,
Colloq. Math. 113 (2008), 119-149.
(doi,
EUDML).
-
Kac's Theorem for weighted projective lines,
Journal of the European Mathematical Society, 12 (2010), 1331-1345.
(doi, math.AG/0512078).
-
Connections for weighted projective lines,
J. Pure Appl. Algebra, 215 (2011), 35-43.
(doi).
-
Poisson structures on moduli spaces of representations,
J. Algebra 325 (2011), 205-215
(doi).
-
Monodromy for systems of vector bundles and multiplicative preprojective algebras,
Bulletin of the London Mathematical Society 45 (2013), 309-317.
(doi)
-
Kac's Theorem for equipped graphs and for maximal rank representations,
Proceedings of the Edinburgh Mathematical Society 56 (2013), 443-447.
(doi,
pdf).
-
Decomposition of pointwise finite-dimensional persistence modules,
Journal of Algebra and Its Applications Vol. 14, No. 5 (2015), 1550066 (8 pages).
(doi,
arXiv:1210.0819 [math.RT]).
-
(With Frédéric Chazal and Vin de Silva)
The observable structure of persistence modules,
Homology, Homotopy and Applications 18 (2016), 247-265.
(doi, pdf)
-
(With Julia Sauter)
On quiver Grassmannians and orbit closures for representation-finite algebras,
Mathematische Zeitschrift 285 (2017), 367–395.
(open access doi)
-
Classification of modules for infinite-dimensional string algebras,
Transactions of the American Mathematical Society,
370 (2018), 3289-3313.
(doi, pdf)
-
Representations of equipped graphs: Auslander-Reiten theory,
in: Proceedings of the 50th Symposium on Ring Theory and Representation Theory.
Held at the University of Yamanashi, October 7–10, 2017. Edited by Katsunori Sanada. Symposium on Ring Theory and Representation Theory Organizing Committee, Yamanashi, 2018.
(pdf,
entire proceedings)
-
(With Raphael Bennett-Tennenhaus)
Σ-pure-injective modules for string algebras and linear relations,
Journal of Algebra 513 (2018), 177-189.
(doi,
pdf)
-
(With Andrew Hubery)
A new approach to simple modules for preprojective algebras,
Algebras and Representation Theory 23 (2020), 1849-1860.
(doi,
arxiv:1803.09482 [math.RT])
-
(With Magnus Bakke Botnan)
Decomposition of persistence modules,
Proceedings of the American Mathematical Society 148 (2020), 4581-4596.
(doi,
arxiv:1811.08946 [math.RT])
-
(With Biao Ma, Baptiste Rognerud and Julia Sauter)
Combinatorics of faithfully balanced modules,
Journal of Combinatorial Theory. Series A. 182 (2021), 105472, 45pp.
(doi,
arXiv:1905.00613 [math.RT])
-
(With Yuta Kimura) On deformed preprojective algebras,
Journal of Pure and Applied Algebra 226 (2022), 107130, 22pp.
(doi,
arXiv:2108.00795)
-
(With Raphael Bennett-Tennenhaus) Semilinear clannish algebras,
Proceedings of the London Mathematical Society (3) 2024;129:e12637, 58pp.
(open access doi)
-
Rigid integral representations of quivers over arbitrary commutative rings,
Annals of Representation Theory, Volume 1 (2024) no. 3, pp. 375-384.
(open access doi)
Preprints
ArXiv author page
Knitting
An applet written by Jan Geuenich (at my request) to compute Auslander-Reiten quivers by the knitting algorithm.
It either computes the preprojective component, or the entire AR quiver if the algebra is of finite representation type and representation-directed.
Call it without an argument to do a random example:
https://www.math.uni-bielefeld.de/~wcrawley/knitting/
The simple modules are labelled by digits or letters.
Place the cursor over a vertex to display the dimension vector of the corresponding indecomposable module,
as a list of simples with appropriate multiplicities.
In general one needs to specify the labels of the simple modules and the dimension vectors of the indecomposable
direct summands of the radicals of their projective covers.
For example the path algebra of quiver
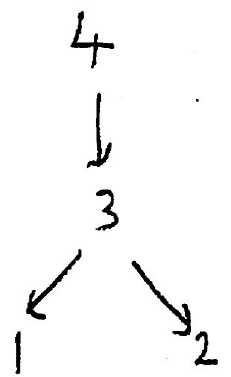 has simples 1,2,3,4 and the radicals of the projective covers P[1] and P[2] are zero, the radical of P[3] is a direct sum of simples 1 and 2 and the radical of P[4]
is indecomposable of dimension vector 123. Compute the AR quiver with
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:,3:1+2,4:123
has simples 1,2,3,4 and the radicals of the projective covers P[1] and P[2] are zero, the radical of P[3] is a direct sum of simples 1 and 2 and the radical of P[4]
is indecomposable of dimension vector 123. Compute the AR quiver with
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:,3:1+2,4:123
The commutative square algebra
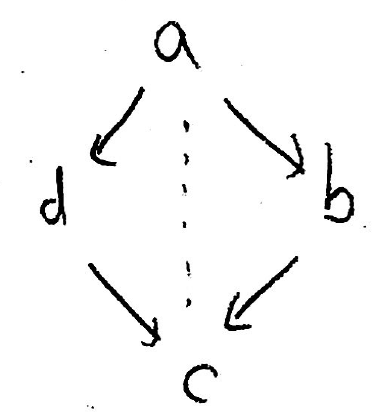 has simples a,b,c,d and rad P[a] is indecomposable of dimension vector bcd, rad P[b] has dimension vector c, rad P[c] is zero and rad P[d] has dimension vector c.
Compute the AR quiver with
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=a:bcd,b:c,c:,d:c
has simples a,b,c,d and rad P[a] is indecomposable of dimension vector bcd, rad P[b] has dimension vector c, rad P[c] is zero and rad P[d] has dimension vector c.
Compute the AR quiver with
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=a:bcd,b:c,c:,d:c
The path algebra of the quiver
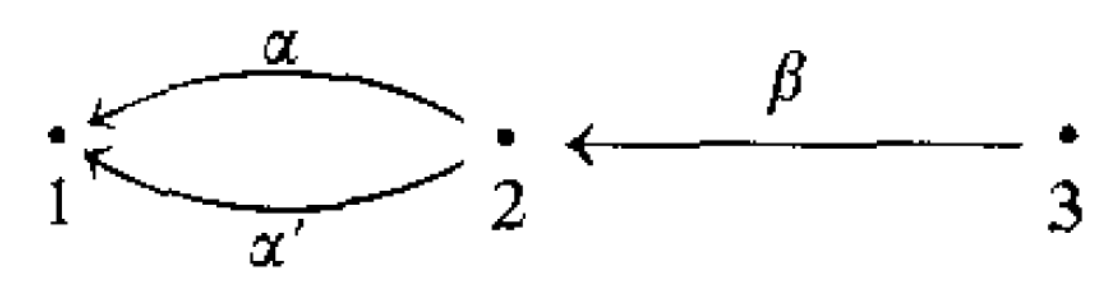 has preprojective component
has preprojective component
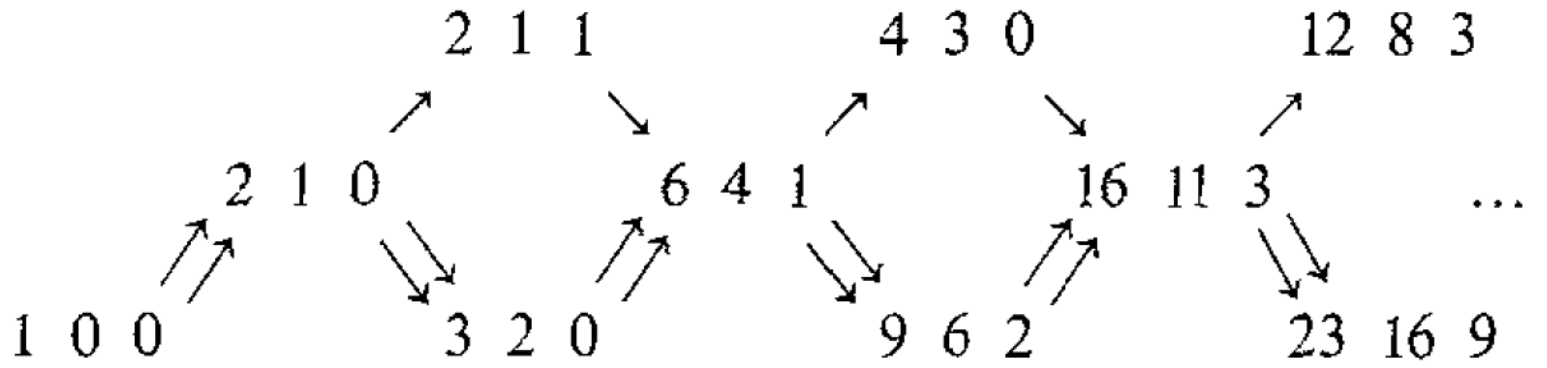 displayed in C. M. Ringel, Finite dimensional hereditary algebras of wild representation type, Mathematische Zeitschrift 161 (1978), 235-255.
Now rad P[1] is zero, rad P[2] has two indecomposable summands of dimension vector 1 and rad P[3] is indecomposable of dimension vector 122,
so the preprojective component is computed with:
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:1+1,3:112
(Find the misprint.)
displayed in C. M. Ringel, Finite dimensional hereditary algebras of wild representation type, Mathematische Zeitschrift 161 (1978), 235-255.
Now rad P[1] is zero, rad P[2] has two indecomposable summands of dimension vector 1 and rad P[3] is indecomposable of dimension vector 122,
so the preprojective component is computed with:
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:1+1,3:112
(Find the misprint.)
You can drag the projective vertices to new positions, or specify them with the option "positions=".
Another example, taken from section 6.6 of P. Gabriel, Auslander-Reiten sequences and representation-finite algebras, in "Representation theory, I"
(Proc. Workshop, Carleton Univ., Ottawa, Ont., 1979), pp. 1–71, Lecture Notes in Math., 831, Springer, Berlin, 1980.
The algebra with quiver
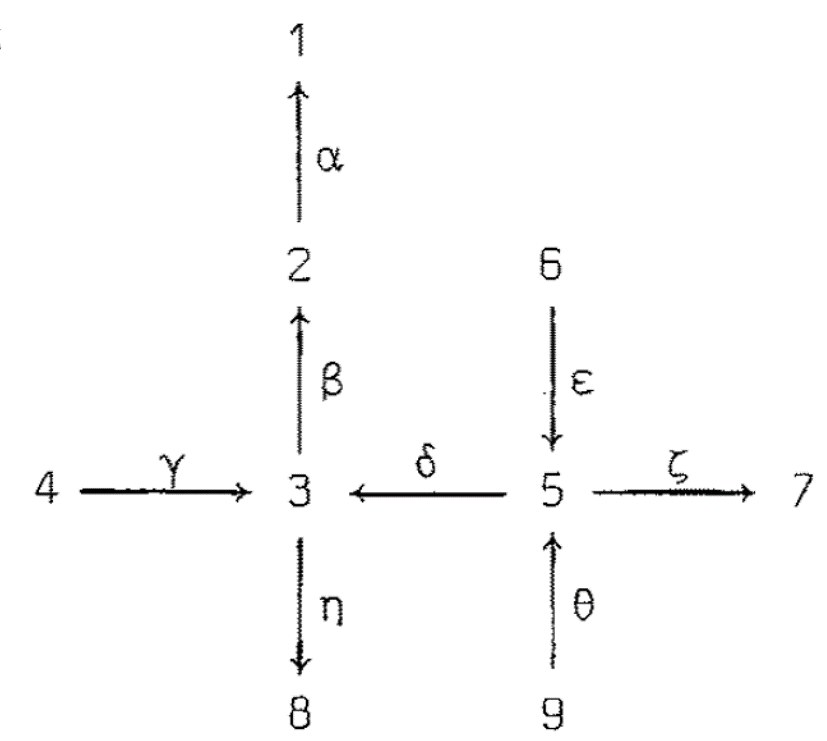 and relations βγ = βδε = ζε = ηδθ = 0 has AR quiver
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:1,3:12+8,4:38,5:1238+7,6:358,7:,8:,9:12357&positions=1:3,2:4,3:5,4:2,5:6,6:0,7:7,8:5.2,9:1
or
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:1,3:12+8,4:38,5:1238+7,6:358,7:,8:,9:12357&positions=1:(-50|0),2:(0|0),3:(50|0),4:(-100|1),5:(100|0),6:(-200|0),7:(150|0),8:(60|0),9:(-150|0)
and relations βγ = βδε = ζε = ηδθ = 0 has AR quiver
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:1,3:12+8,4:38,5:1238+7,6:358,7:,8:,9:12357&positions=1:3,2:4,3:5,4:2,5:6,6:0,7:7,8:5.2,9:1
or
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:1,3:12+8,4:38,5:1238+7,6:358,7:,8:,9:12357&positions=1:(-50|0),2:(0|0),3:(50|0),4:(-100|1),5:(100|0),6:(-200|0),7:(150|0),8:(60|0),9:(-150|0)
You can draw the AR quiver vertically with the option "orientation=vertical".
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:1,3:12+8,4:38,5:1238+7,6:358,7:,8:,9:12357&positions=1:(-50|0),2:(0|0),3:(50|0),4:(-100|1),5:(100|0),6:(-200|0),7:(150|0),8:(60|0),9:(-150|0)&orientation=vertical
Note that it is assumed that the base field is algebraically closed, or more generally that every simple module has endomorphism algebra equal to the base field
(equivalently that the algebra is given by a quiver with admissible relations).
Archived materials
- Lectures on representation theory and invariant theory
(pdf).
A graduate course given in 1989/90 at Bielefeld University.
This is an introduction to the representation theory of the symmetric
and general linear groups (in characteristic zero), and to classical
invariant theory.
List of corrections.
- Lectures on representations of quivers
(pdf |
scanned pdf - includes one extra diagram).
A graduate course given in 1992 at Oxford University.
This is an introduction to the representation
theory of quivers, and in particular the representation theory of extended
Dynkin quivers.
List of corrections.
- More lectures on representations of quivers
(scanned pdf).
Another graduate course from 1992 at Oxford University.
More about representations of quivers, including Auslander-Reiten
theory, results of Kerner and of Schofield.
- Geometry of representations of algebras
(pdf).
A graduate course given in 1993 at Oxford University.
This is a survey of how algebraic
geometry has been used to study representations of algebras (and quivers
in particular).
- Cohomology and central simple algebras
(pdf).
An MSc course given in 1996 at Leeds University.
An introduction to homological algebra
and applications to central simple algebras.
- Representations of quivers, preprojective algebras and
deformations of quotient singularities
(pdf).
Lectures from a DMV Seminar in May 1999 on "Quantizations
of Kleinian singularities" organized by R. Buchweitz, P. Slodowy
and myself at Oberwolfach.
Here is the group photo from the meeting.
(There are mistakes in Lemma 4.5 and the proof of Theorem 5.9.
The first of these has been sorted out independently by P. Etingof
and V. Ginzburg in math.AG/0011114.
For the second, the proof elsewhere in the literature is correct.)
- The website
from a Summer School on "Geometry of Quiver-representations and Preprojective
Algebras" (Isle of Thorns/UK, September 10 - 17, 2000)
- An unfinished and abandoned paper
on generic deformed preprojective algebras
(pdf),
dating from the late 1990s,
and mentioned by P. Etingof and E. Rains in
math.RT/0503393.
- The website
for a conference in honour of John McConnell and Chris Robson
(Leeds, May 5-6, 2006)
- The slides of a talk in Glasgow in November 2014 on
"Two applications of the functorial filtration method".
- Notes for a working seminar on "Sylvester rank functions for rings and universal localization" in June 2021.
Past and Future Meetings
-
International AsiaLink conference on Algebras and Representations
(Beijing Normal University, May 23--28, 2005)
-
Journées Solstice d'été 2005 : Groupes
(Paris, June 23-25, 2005)
-
Interactions
between noncommutative algebra and algebraic geometry (Banff,
September 10-15, 2005)
-
Workshop
in Non-Commutative Geometry (Copenhagen, November 7-10, 2005)
-
Sklyanin Algebras and Beyond
(Leeds, December 16-17, 2005)
-
Ring Theory: recent progress and applications
(Leeds, May 5-6, 2006)
-
Interactions
between Algebraic Geometry and Noncommutative Algebra
(Oberwolfach, May 7-13, 2006)
-
Workshop
on algebraic vector bundles (Münster, June 26-30, 2006)
-
Workshop
on Triangulated Categories (Leeds, August 13-19, 2006)
-
International Congress of Mathematicians
(Madrid, August 22-30, 2006)
-
Representations
of Quivers, Singularities and Lie Theory
(Beijing, September 13-17, 2006)
-
Representations
of Algebras and their Geometry (Paderborn, November 10-11, 2006)
-
Recent
developments in the theory of Hall algebras (CIRM, Luminy, France, November 20-24, 2006)
-
Trends in Noncommutative Geometry
(Newton Institute, Cambridge, December 18-22, 2006)
-
Perspectives in Auslander-Reiten Theory.
On the occasion of the 65th birthday of Idun Reiten
(Trondheim, May 10-12, 2007)
-
Arithmetic
harmonic analysis on character and quiver varieties
(American Institute of Mathematics, Palo Alto, June 4-8, 2007)
-
XII International Conference on Representations of Algebras and Workshop
(Torun, August 15-24, 2007)
-
Representation
Theory of Finite Dimensional Algebras (Oberwolfach, February 17-23, 2008)
-
Maurice
Auslander Distinguished Lectures and International Conference (Woods
Hole, Cape Cod, April 25-27, 2008)
-
Symmetries in Mathematics and
Physics, in honor of Victor Kac (Cortona, June 22-28, 2008)
-
XIII International
Conference on Representations of Algebras and Workshop
(Sao Paulo, July 30-August 8, 2008)
-
Minisymposium on Algebras
(Uppsala, February 20, 2009)
-
Combinatorial
Geometric Structures in Representation Theory
(Durham, July 6-16, 2009)
-
Summer school on Geometry of representations
(Cologne, July 26-31, 2009)
-
Workshop on Noncommutative Algebraic Geometry and Related Topics
(Manchester, August 3-7, 2009)
-
Quiver
varieties, Donaldson-Thomas invariants and instantons
(CIRM, Luminy, September 14-18, 2009)
-
Interplay
between representation theory and geometry (Beijing, May 3-7, 2010)
-
Interactions
between Algebraic Geometry and Noncommutative Algebra (Oberwolfach, May 9-15, 2010)
-
XIV International Conference on Representations of Algebras and Workshop
(Tokyo, August 6-15, 2010)
-
Representation
Theory of Quivers and Finite Dimensional Algebras (Oberwolfach, February 20-26, 2011)
-
New developments
in noncommutative algebra and its applications (Isle of Skye, June 26-July 2, 2011)
-
Cluster
categories and cluster tilting. A conference honoring Idun
Reiten on the occasion of her 70th birthday (Trondheim, March 28-30, 2012)
-
Representation
Theory and Geometry (Zurich, April 10-14, 2012)
-
Workshop
and International Conference on Representations of Algebras (ICRA 2012) (Bielefeld, August 8-17, 2012)
-
Introductory Workshop: Noncommutative Algebraic Geometry and Representation Theory
(MSRI, Berkeley, January 28-February 1, 2013)
-
Representation Theory, Homological Algebra, and Free Resolutions
(MSRI, Berkeley, February 11-17, 2013)
-
Interactions between Noncommutative Algebra, Representation Theory, and Algebraic Geometry
(MSRI, Berkeley, April 8-12, 2013)
-
Representation Theory of Quivers and Finite Dimensional Algebras
(Oberwolfach, February 16-22, 2014)
-
Interactions between Algebraic Geometry and Noncommutative Algebra
(Oberwolfach, May 18-24, 2014)
-
XVI International Conference on Representations of Algebras (ICRA 2014)
(Sanya, Hainan Province, China, August 20-29, 2014)
-
Representation Theory (Mittag-Leffler Institute, Sweden, Spring 2015)
-
Summer School on Koszul Duality (Bad Driburg, Germany, August 10-14, 2015)
-
Derived structures in geometry and representation theory (Oxford, August 31- September 4, 2015)
-
Infinite-dimensional Representations of Finite-dimensional Algebras (Manchester, September 9-17, 2015)
-
Representations of Algebraic Groups, in honour of Stephen Donkin (York, July, 13-15, 2016)
-
XVII International Conference on Representations of Algebras (ICRA 2016) (Syracuse, USA, August 10-19, 2016)
-
Representation Theory of Quivers and Finite Dimensional Algebras (Oberwolfach, February 19-25, 2017)
-
Triangulated categories and geometry - a conference in honour of Amnon Neeman
(Bielefeld, May 15-19, 2017)
-
BIREP Summer School on Gentle Algebras
(Bad Driburg, Germany, August 14–18, 2017)
-
Noncommutative Algebraic Geometry and Related Topics
(RIMS, Kyoto, Japan, September 25-29, 2017)
-
50th Symposium on Ring Theory and Representation Theory (Yamanashi, Japan, October 7-10, 2017)
[another link]
-
Workshop "Discrete Categories in Representation Theory" (Bielefeld, April 20-21, 2018)
-
Maurice Auslander Distinguished Lectures and International Conference (Woods Hole, Massachusetts, USA,
April 25 - 30, 2018)
-
Interactions between Algebraic Geometry and Noncommutative Algebra
(Oberwolfach, May 27-June 2, 2018)
-
XVIII International Conference on Representations of Algebras (ICRA 2018)
(Charles University, Prague, Czech Republic, August 8-17, 2018)
-
Interactions
between commutative algebra, representation theory, and algebraic geometry;
A conference in memoriam Ragnar-Olaf Buchweitz
(Münster, March 19-23, 2019)
-
Computational
Applications of Quiver Representations: TDA and QPA
(Bielefeld University, May 2-4, 2019)
-
Summer
school on Persistent homology and Barcodes
(JLU Gießen – Schloß Rauischholzhausen, August 5-9, 2019)
-
BIREP Summer School on Cohen–Macaulay Modules in Representation Theory (Bad Driburg, Germany, August 12–16, 2019)
-
Representation Theory in Bielefeld – Past and Future (Bielefeld University, September 24-25, 2019)
-
Anniversary Conference — 50 Years Faculty Of Mathematics (Bielefeld University, September 26-27, 2019)
-
Algebraic Representation Theory and Related Topics (Sanya, Hainan Province, China, October 7-11, 2019)
-
Representation Theory of Quivers and Finite Dimensional Algebras (Oberwolfach, January 19-25, 2020)
-
Birthday Colloquium (ICMS Edinburgh/Zoom, September 10, 2020)
-
Fourth International Colloquium on Representations
of Algebras and Its Applications; Alexander Zavadskij (Online / Bogota, Colombia, November 4-6, 2020)
-
XIX International Conference on Representations of Algebras (ICRA 2020) online meeting
(Online, November 9-27, 2020). (The meeting in Trieste was cancelled)
-
Virtual ARTA 2021 Advances in Representation Theory of Algebras (Online, May 17-28, 2021)
-
2021 London Mathematical Society Northern Regional Meeting and Conference (University of Manchester, September 1-10, 2021)
-
Representations of Algebras and Sheaves (ZiF Bielefeld, November 13, 2021)
-
Flash Talks in Representation Theory at NTNU (Online, January 4, 2022)
-
Representation Theory and Geometry (RepTheoGeometry2022 at Queen's-RMC) (Online, February 14-16, 2022)
-
Geometry and Representations (ZiF Bielefeld, April 9, 2022)
-
Interactions between Algebraic Geometry and Noncommutative Algebra
(Oberwolfach, May 1-7, 2022)
-
Representation Theory and Triangulated Categories (Bielefeld, September 26-30, 2022)
-
Algebras and Representation Theory Network Meeting (Cologne, January 27-28, 2023)
-
Representation Theory of Quivers and Finite-Dimensional Algebras
(Oberwolfach, February 12-18, 2023)
-
ARTIG 2 - Algebras and Representation Theory in Germany (Stuttgart, June 23-24, 2023)
-
Homological Algebra and Representation Theory
(Karlovasi, Samos, July 10-14, 2023)
-
ARTIG 3 - Representation Theory and Non-Commutative Geometry
(Paderborn, December 1-2, 2023)
-
ARTIG 4 - Algebras and Representation Theory
(Aachen, June 14-15, 2024)
-
International Conference on Representations of Algebras ICRA 21
(Shanghai, China, July 31-August 9, 2024)
-
Integral Structures in Geometry and Representation Theory (Paderborn, September 9-13, 2024). With a session on Tame categories, geometric models, and homological mirror symmetry.
-
Colloquium in Honour of Lutz Hille
(Bielefeld, November 15, 2024)
-
ARTIG 5 - Algebras and Representation Theory in Germany
(Bonn, February 14-15, 2025)
-
Winter School "Large Modules and Endofiniteness"
(Stuttgart, February 24-28, 2025)
-
Workshop on bricks and endofinite representations
(Bielefeld, March 3-5, 2025)
-
ARTIG 6 Conference
(Bochum, July 10-11, 2025)
-
Conference on the legacy of Peter Gabriel (Bielefeld, August 25-29, 2025)
-
ARTIG 7 - Algebras and Representation Theory in Germany
(Munich, December 12-13, 2025)
-
Representation theory of Finite Groups, Schur and Hall Algebras in Honour of Sandy Green (York, June 3-5, 2026)



 In recent years I have concentrated on representations of quivers and
preprojective algebras. A quiver is essentially the same
thing as a directed graph,
and a representation associates a vector space to each vertex
and a linear map to each arrow. The subject was started by P. Gabriel
in 1972, when he discovered that the
quivers with only finitely many indecomposable representations are exactly
the ADE Dynkin diagrams which occur in Lie theory (for example a quiver of
type
E6 is illustrated on the left).
Quivers and their representations now appear in all sorts of
areas of mathematics and physics,
including representation theory, cluster algebras, geometry (algebraic,
differential, symplectic), noncommutative geometry,
quantum groups, string theory, and more.
In recent years I have concentrated on representations of quivers and
preprojective algebras. A quiver is essentially the same
thing as a directed graph,
and a representation associates a vector space to each vertex
and a linear map to each arrow. The subject was started by P. Gabriel
in 1972, when he discovered that the
quivers with only finitely many indecomposable representations are exactly
the ADE Dynkin diagrams which occur in Lie theory (for example a quiver of
type
E6 is illustrated on the left).
Quivers and their representations now appear in all sorts of
areas of mathematics and physics,
including representation theory, cluster algebras, geometry (algebraic,
differential, symplectic), noncommutative geometry,
quantum groups, string theory, and more.
 The preprojective algebra associated to
a quiver was invented by I. M. Gelfand and V. A. Ponomarev.
Its modules are intimately related to representations of the quiver, but it is
often the modules for the preprojective algebra which are of relevance in other
parts of mathematics. There is beautiful geometry linked to the preprojective algebra,
including Kleinian singularities and H. Nakajima's quiver varieties. (The
illustration on the right shows the real-valued points of
varieties associated to a quiver of extended Dynkin, that is,
affine, type D4.)
The preprojective algebra associated to
a quiver was invented by I. M. Gelfand and V. A. Ponomarev.
Its modules are intimately related to representations of the quiver, but it is
often the modules for the preprojective algebra which are of relevance in other
parts of mathematics. There is beautiful geometry linked to the preprojective algebra,
including Kleinian singularities and H. Nakajima's quiver varieties. (The
illustration on the right shows the real-valued points of
varieties associated to a quiver of extended Dynkin, that is,
affine, type D4.) There are also links between the preprojective algebra and
the classification of differential equations on the Riemann
sphere. They are used in work on the Deligne-Simpson problem,
which concerns the existence of matrices
in prescribed conjugacy classes whose product is
the identity matrix, or whose sum is the zero matrix.
(The picture on the left shows loops on the punctured Riemann sphere which
generate its fundamental group. Consideration of the monodromy around
such loops links
the classification of differential equations on the Riemann sphere
to the Deligne-Simpson problem.)
There are also links between the preprojective algebra and
the classification of differential equations on the Riemann
sphere. They are used in work on the Deligne-Simpson problem,
which concerns the existence of matrices
in prescribed conjugacy classes whose product is
the identity matrix, or whose sum is the zero matrix.
(The picture on the left shows loops on the punctured Riemann sphere which
generate its fundamental group. Consideration of the monodromy around
such loops links
the classification of differential equations on the Riemann sphere
to the Deligne-Simpson problem.)
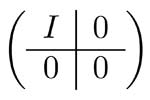 One way to study tame algebras is to convert the problem of classifying their
modules into a matrix problem: putting a partitioned matrix into
canonical form using not all elementary operations, but a subset defined
by the partition.
(The illustration on the right shows what an arbitrary matrix can be
reduced to if you allow all row and column operations; it also shows an
example of a partition of a matrix.)
Using advanced methods based on this idea, Yu. A. Drozd
proved
his wonderful Tame and Wild Theorem showing that there is a wide gulf between
the behaviour of tame and wild algebras.
The same methods can be used to show that tame algebras are characterized by
the behaviour of their infinite-dimensional modules. In fact, the behaviour of
infinite-dimensional modules for tame algebras is extremely interesting, and
not at all understood.
One way to study tame algebras is to convert the problem of classifying their
modules into a matrix problem: putting a partitioned matrix into
canonical form using not all elementary operations, but a subset defined
by the partition.
(The illustration on the right shows what an arbitrary matrix can be
reduced to if you allow all row and column operations; it also shows an
example of a partition of a matrix.)
Using advanced methods based on this idea, Yu. A. Drozd
proved
his wonderful Tame and Wild Theorem showing that there is a wide gulf between
the behaviour of tame and wild algebras.
The same methods can be used to show that tame algebras are characterized by
the behaviour of their infinite-dimensional modules. In fact, the behaviour of
infinite-dimensional modules for tame algebras is extremely interesting, and
not at all understood.
 has simples 1,2,3,4 and the radicals of the projective covers P[1] and P[2] are zero, the radical of P[3] is a direct sum of simples 1 and 2 and the radical of P[4]
is indecomposable of dimension vector 123. Compute the AR quiver with
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:,3:1+2,4:123
has simples 1,2,3,4 and the radicals of the projective covers P[1] and P[2] are zero, the radical of P[3] is a direct sum of simples 1 and 2 and the radical of P[4]
is indecomposable of dimension vector 123. Compute the AR quiver with
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:,3:1+2,4:123
 has simples a,b,c,d and rad P[a] is indecomposable of dimension vector bcd, rad P[b] has dimension vector c, rad P[c] is zero and rad P[d] has dimension vector c.
Compute the AR quiver with
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=a:bcd,b:c,c:,d:c
has simples a,b,c,d and rad P[a] is indecomposable of dimension vector bcd, rad P[b] has dimension vector c, rad P[c] is zero and rad P[d] has dimension vector c.
Compute the AR quiver with
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=a:bcd,b:c,c:,d:c
 has preprojective component
has preprojective component
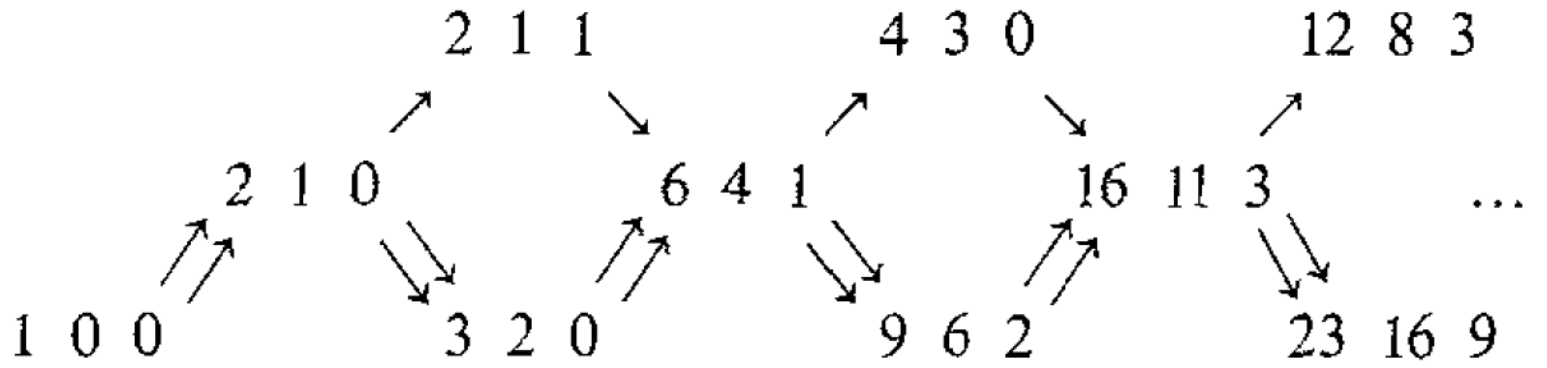 displayed in C. M. Ringel, Finite dimensional hereditary algebras of wild representation type, Mathematische Zeitschrift 161 (1978), 235-255.
Now rad P[1] is zero, rad P[2] has two indecomposable summands of dimension vector 1 and rad P[3] is indecomposable of dimension vector 122,
so the preprojective component is computed with:
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:1+1,3:112
(Find the misprint.)
displayed in C. M. Ringel, Finite dimensional hereditary algebras of wild representation type, Mathematische Zeitschrift 161 (1978), 235-255.
Now rad P[1] is zero, rad P[2] has two indecomposable summands of dimension vector 1 and rad P[3] is indecomposable of dimension vector 122,
so the preprojective component is computed with:
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:1+1,3:112
(Find the misprint.)
 and relations βγ = βδε = ζε = ηδθ = 0 has AR quiver
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:1,3:12+8,4:38,5:1238+7,6:358,7:,8:,9:12357&positions=1:3,2:4,3:5,4:2,5:6,6:0,7:7,8:5.2,9:1
or
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:1,3:12+8,4:38,5:1238+7,6:358,7:,8:,9:12357&positions=1:(-50|0),2:(0|0),3:(50|0),4:(-100|1),5:(100|0),6:(-200|0),7:(150|0),8:(60|0),9:(-150|0)
and relations βγ = βδε = ζε = ηδθ = 0 has AR quiver
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:1,3:12+8,4:38,5:1238+7,6:358,7:,8:,9:12357&positions=1:3,2:4,3:5,4:2,5:6,6:0,7:7,8:5.2,9:1
or
https://www.math.uni-bielefeld.de/~wcrawley/knitting/?projectives=1:,2:1,3:12+8,4:38,5:1238+7,6:358,7:,8:,9:12357&positions=1:(-50|0),2:(0|0),3:(50|0),4:(-100|1),5:(100|0),6:(-200|0),7:(150|0),8:(60|0),9:(-150|0)